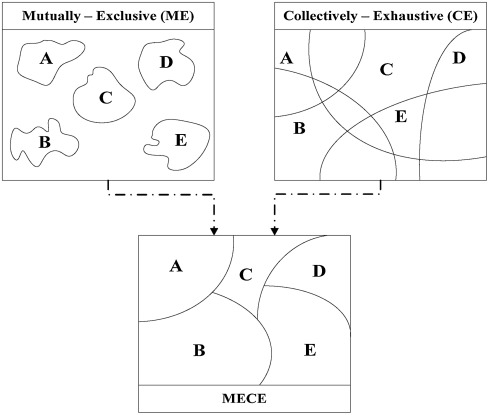
대학 때 활동하던 동아리에서 거의 OS급으로 모든 구성원들이 뇌에 반강제로 설치당하던 프레임웍이 있다. MECE. Mutually-Exclusive, Collectively-Exhaustive. 이해를 위해 의역하자면 '(조각, 개체들) 서로는 배타적이게(겹치지 않게), (조각들을) 다 모았을 땐 전체에서 빠진 부분이 없게(흠결이 없게)'쯤으로 해석된다.
https://www.sciencedirect.com/science/article/abs/pii/S1568494617302375
그 당시 동아리 내 하위 분과 중에는 'Critical Reasoning' 이라는, 이름도 무시무시한 논리덕후들의 집합소가 있었다. 대충 일상대화를 할 줄 모르거나, 이쪽에서 훈련되지 않은 상태에서 억지로 처음 대화를 해보면 기분이 나빠지는 애들 쯤으로 생각하면 된다. 나를 비롯한 다른 분과의 선후배들은 '쟤네의 선조들이 옛날에 스터디 도중 어디서 또 피곤한 말을 물어왔구나'쯤으로 생각했지만, 그래도 그 당시 기준으로도 꽤 오래전부터 동아리 전체에서 채택되어 신입부터 교육받던 프레임웍이었다. 우리는 저 툴을 논리적인 사고와 대화를 위해 주제 혹은 개체를 세부적으로 구성하는 기술 정도로 여겼었다. 나중에 알고 보니 과학 전반 또는 의학에서도 당연하게 쓰이는 툴이었지만.
동아리 내외적으로 발표나 논문에서 어떤 집단을 나눌 때, 어떤 개체나 현상을 쪼개서 개요를 짜고 분석할 때, 일단 저 툴을 통과하지 못하면 처음부터 기준 자체가 틀려먹었기 때문에 엉성하고 부정확한 전개가 될, 폐기 대상이었다. 그래서 우린 한참 시간과 에너지를 쏟아붓다가 나중에 가서야 엎어질 위험을 줄이고자 처음부터 저 밑그림을 큼직하게라도 정확하게 잡는 것이 습관이 되었다.
ME(Mutually-Exclusive)와 CE(Collectively-Exhaustive)는 각각의 한계를 지니고 있다. 전체 사각형을 전체집합(U)으로 봤을 때, ME하게 눈앞에 보이는 하나씩만 우선 개체로 지정해 버리면 전체집합에서 설명하지 못하는 구멍이 숭숭 뚫린다. 주로 프로젝트나 회의의 구상 단계에서 '생각나는 대로 뱉기'로 개요를 쭉 짜서 진행까지 해버렸을 때 발생하는 현상이다. 아무리 여러 가지를 고려해서 다 넣은 것처럼 보여도 분명히 구멍은 있고, 일을 진행하면 할수록 그 구멍은 끔찍하게도 많이 발견된다. 그리고 그 결과로 나온 어떤 것은 굉장히 불완전한 것이 된다. 당연하게도.
CE는 반대로 개별 개체의 고유성, 혹은 배타성을 전혀 고려하지 않고 오로지 '기준' 한 가지에만 경도되었을 때 일어나는 현상이다. 타겟 집단에 대한 기준이 각각 한 가지일 때는 문제가 없는 것처럼 보인다. 성별, 연령, 지역, 물질/비물질 등. 각각의 기준이 따로 존재할 땐 그 기준을 중심으로 자연스럽게 MECE 한 틀이 꽉꽉 채워진다. 다만 그 기준이 성별*연령*지역 이런 식으로 다중 다축의 매트릭스가 되면 그땐 그림 중 오른쪽 위의 CE 그림처럼 중첩이 생긴다. 이럴 땐 주로 일의 중반부쯤 여기저기에서 했던 일을 또 하는 상황이 반복되고, 후반부의 솔루션쯤 가면 솔루션이 4개인데 사실 겹치는 것끼리 뭉쳐놓고 보면 2개(...)나 될법한 그런 있으나 마나 한 일 혹은 결과가 된다.
프레임웍을 이식받다가 이 지점에 다다르면 '그럼 MECE한게 좋다면서 애초에 ME, CE 둘 다 문제라면 어떻게 하라는 거냐'라는 질문에 부딪친다. 방법은 어느 한쪽에서부터라도 시작해서 다른 쪽을 거치면 된다. 어지간히 기계적 사고가 익숙한 게 아닌 이상, 우리 대부분은 맞는지 틀린 건지도 모를 기준점을 냅다 그으면서 CE에서 출발하는 것보단 차라리 ME에서 시작하는 게 낫다. ME. 생각나는 대로 뱉어본다. 그 자체가 문제는 아니다. 그리고 튀어나온 개체들에 해쉬나 태그를 붙인다. 그렇게 하다 보면 개체 사이에 어느 정도의 공통분모, 공약수, 최소공배수와 비슷한 친원성이 생긴다. 그때쯤 거기서 공통적으로 잡힌 것들을 한 단계 메타로 올려서 '기준'이라는 걸 만든다. 그 기준을 잡아낼 때마다 CE처럼 전체 도화지(주제, 목표, 개념 등등)를 나누는 선을 그어본다. 아마 기준이 세 개만 되어도 거의 무조건 중첩은 생긴다. 그럼 그때 ME적 관점에서 중첩을 없앨만한 조정을 하면 된다. 기준을 수정해서 중첩 자체가 사라지는 게 제일 좋고, 그게 도저히 안 되면 중첩되는 그 대상에게 독립된 개체로서 고유한 식별자를 부여하는 방식.
당연하지만 우리가 살아가고 또한 일적으로도 해결해야하는 현실은 거의 항상 MECE 하지 않다. 대부분의 현실은 ME와 CE 사이 어딘가에 있다. 이것들 만으로는 모든 게 설명되진 않는(ME), 그게 꼭 그 문제라고만 할 수는 없는(CE) 일들이 투성이니까. 설령 MECE 하게 보이도록 최대한 체계적으로 이론화, 단순화해서 일이나 연구를 진행한다고 해도 그건 현실의 불완전한 거울일 뿐 완벽한 투영은 될 수 없다. 다만 그 한계를 확실히 인정하고, 완벽에 도달할 순 없지만 최대한 가까워진다는 느낌으로 겹치거나 빈 공간을 지워나가는 거다. 그러다 보면 그 일은 허용가능한 오차범위 내에서 모든 구성요소가 전체집합을 이루는 것에 겹침도 없고 남김도 없게 기여하게 된다.
물론 끝을 모르던 이상주의에서 한발짝이라도 벗어났을 무렵부터 느낀 다른 한계도 있다. 저 네모난 도화지가 전체집합(U)이 아닐 경우. 사실은 네모난 도화지 바깥에 그것을 에워싸는 하나의 네모가 또 있고, 그게 전체집합(U)이며, 안의 도화지 네모와 바깥의 전체집합(U)의 사이엔 여집합(c)이 있을 수도 있다는 것. 내가 처음부터 이 도화지를 그린다는 것 자체가 틀렸을 경우, 바깥의 모든 게 처음부터 참이 아닌 정보였을 경우, 그러거나 말거나 그냥 안 되거나, 그도 아니면 내가 열심히 머리를 굴린 것과는 전혀 다르게 흥미로운(?) 전개로 튀는 경우. 일에서는 이 여집합의 가능성을 최대한 줄이려, 다른 말로는 안쪽의 네모난 MECE 도화지의 면적을 넓히려 노력한다. 나 포함 여러 사람의 밥줄을 기도메타에 의지할 순 없으니까. 일이 아닌 현실에서도 마찬가지이긴 한데, 다소 양가적인 감정이 든다. 어떤 때는 저 여집합이 무섭기도, 무기력하게 만들기도 하고, 또 어떤 때는 그 여집합 때문에 말도 안되게 좋을 때도 있고. 사람으로 사는 건 때론, 혹은 꽤 자주 쉽지 않다.